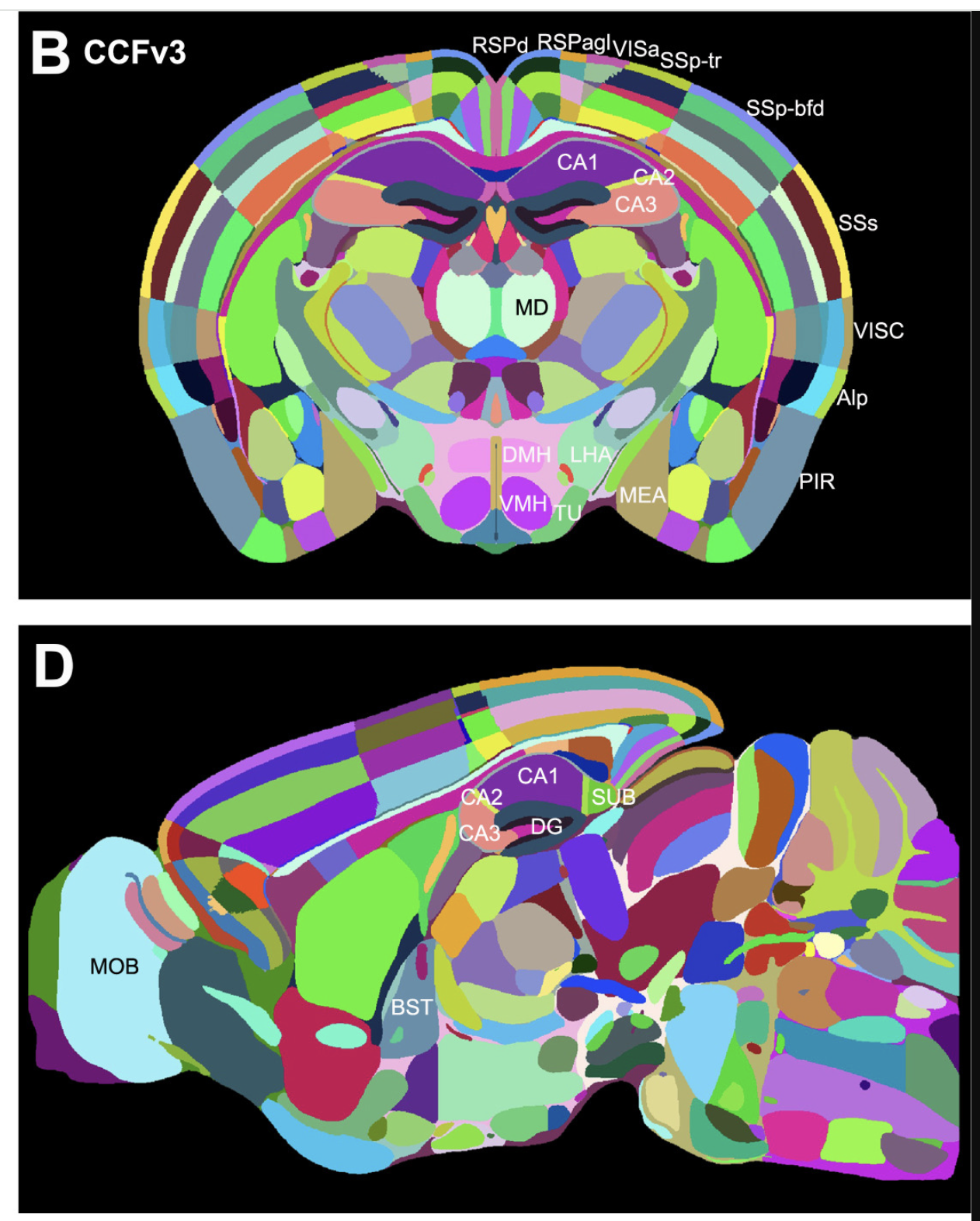
Common Coordinate Framework#
The Allen Mouse Brain Common Coordinate Framework (CCF) is a 3D reference space that was defined by creating an average brain at 10um voxel resolution from serial two-photon tomography images of 1,675 young adult C57Bl6/J mice. This space allows us to attach coordinates to any point or structure in the brain. Using multimodal reference data, we parcellated the entire brain directly in 3D, labeling every voxel with a brain structure spanning 43 isocortical areas and their layers, 314 subcortical gray matter structures, 81 fiber tracts, and 8 ventricular structures. The CCF enables the integration of data across modalities that have been registered into the common space. [Wang et al., 2020]
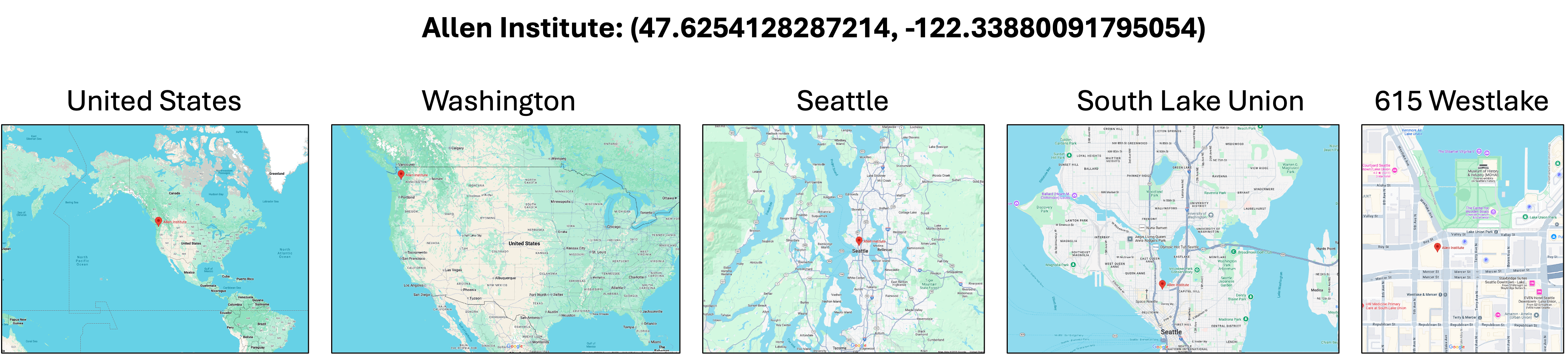
A good analogy for the CCF is geographic coordinates. The Allen Institute has geographic coordinates of (47.6254128287214, -122.33880091795054). This allows us to pinpoint it on a globe or a map. We can also annotate this location at different levels of resolution, saying it is located in the United States or Washington state or Seattle or Westlake Ave. Depending on what you are doing, you might prefer to ask about different levels of the geographic hierarchy.
Likewise, an example neuron in the brain has CCF coordinates of (4625.3821881875, 2534.79472175, 2977.33168800001). We can pinpoint this in the brain, and we can annotate it’s location as being in the Isocortex, the Somatosenory areas, the Primary somatosensory area, or the Primary somatosensory area, mouth. And again, depending on the context, you might choose to use different levels of the CCF hierarchy to describe its location. You might be looking for all neurons in the Somatosensory areas to compare against those in Motor areas, or you might want to compare mouth neurons in the primary somatosensory area to the nose neurons.

In the data here, the CCF is used in a few ways. One, is to specify the location of ephys units. This localization is done post-hoc, when the probe tract is imaged and registered to the CCF. This allows scientists to assign brain structure locations to the sorted units. The second is for the single cell whole brain reconstruction data. During image processing, the brain is registered to the CCF, allowing each node of the skeleton to be mapped to a brain structure. This allows scientists to know where each soma is located, what structures its dendrites originate in, and where its axons project to.
The brain structures are named according to the Allen Reference Atlas Ontology. This is a hierarchical ontology, in which structures are divided into more precise structures at different levels of the hierarchy. Each structure has a name, and unique id, and a list of parent structures that are above it in the hierarchy.
We are using tools from BrainGlobe to help navigate this ontology [Claudi et al., 2020].
from pprint import pprint
import brainglobe_atlasapi as atlasapi
from brainglobe_atlasapi import BrainGlobeAtlas
import os
data_dir = '/root/capsule/data/.brainglobe'
if not os.access(data_dir, os.R_OK):
print('Access error: permissions')
atlasapi.config.write_config_value('brainglobe_dir', '/root/capsule/data/.brainglobe')
First we import the atlas we want to use. There are multiple resolutions available, but for exploring the ontology we can use any. Here we’ll use the 25um version.
atlas = BrainGlobeAtlas('allen_mouse_25um')
We can quickly look at a dataframe of all the structures:
atlas.lookup_df
| acronym | id | name | |
|---|---|---|---|
| 0 | root | 997 | root |
| 1 | grey | 8 | Basic cell groups and regions |
| 2 | CH | 567 | Cerebrum |
| 3 | CTX | 688 | Cerebral cortex |
| 4 | CTXpl | 695 | Cortical plate |
| ... | ... | ... | ... |
| 835 | V3 | 129 | third ventricle |
| 836 | AQ | 140 | cerebral aqueduct |
| 837 | V4 | 145 | fourth ventricle |
| 838 | V4r | 153 | lateral recess |
| 839 | c | 164 | central canal, spinal cord/medulla |
840 rows × 3 columns
Each structure has an acronym, an id, and a name.
Let’s look at one in more detail - we’ll look at VISp
pprint(atlas.structures["VISp"])
{'acronym': 'VISp',
'id': 385,
'mesh': None,
'mesh_filename': PosixPath('/root/capsule/data/.brainglobe/allen_mouse_25um_v1.2/meshes/385.obj'),
'name': 'Primary visual area',
'rgb_triplet': [8, 133, 140],
'structure_id_path': [997, 8, 567, 688, 695, 315, 669, 385]}
Here we see a little more information. There’s the acronym, id, and name. There is information on the mesh for this structure. The “rgb_triplet” is the color used to plot this structure when using the CCF colors. And finally the structure_id_path is the list of parent structures. Let’s see what these are, starting from the end:
pprint(atlas.structures[780])
pprint(atlas.structures[703])
pprint(atlas.structures[688])
{'acronym': 'PA',
'id': 780,
'mesh': None,
'mesh_filename': PosixPath('/root/capsule/data/.brainglobe/allen_mouse_25um_v1.2/meshes/780.obj'),
'name': 'Posterior amygdalar nucleus',
'rgb_triplet': [151, 236, 147],
'structure_id_path': [997, 8, 567, 688, 703, 780]}
{'acronym': 'CTXsp',
'id': 703,
'mesh': None,
'mesh_filename': PosixPath('/root/capsule/data/.brainglobe/allen_mouse_25um_v1.2/meshes/703.obj'),
'name': 'Cortical subplate',
'rgb_triplet': [138, 218, 135],
'structure_id_path': [997, 8, 567, 688, 703]}
{'acronym': 'CTX',
'id': 688,
'mesh': None,
'mesh_filename': PosixPath('/root/capsule/data/.brainglobe/allen_mouse_25um_v1.2/meshes/688.obj'),
'name': 'Cerebral cortex',
'rgb_triplet': [176, 255, 184],
'structure_id_path': [997, 8, 567, 688]}
This is a somewhat tedious way to move through the hierarchy. Here’s a function that lists the acronyms of the list of parent (or ancestor) structures
atlas.get_structure_ancestors("VISp")
['root', 'grey', 'CH', 'CTX', 'CTXpl', 'Isocortex', 'VIS']
And to see the descendants:
atlas.get_structure_descendants("VISp")
['VISp1', 'VISp2/3', 'VISp4', 'VISp5', 'VISp6a', 'VISp6b']
Note: you can pass these functions either the structure acronym or the structure ID.
This can be very valuable if you are look for any neurons that are located in a given structure (again, say VISp) regardless of layer, but they are labeled by the finest parcellation possible. This can give you the full list of structure IDs to include in your search.
To see the entire structure of the tree you can use
atlas.structures
Show code cell output
root (997)
├── VS (73)
│ ├── AQ (140)
│ ├── V3 (129)
│ ├── V4 (145)
│ │ └── V4r (153)
│ ├── VL (81)
│ │ ├── SEZ (98)
│ │ └── chpl (108)
│ └── c (164)
├── fiber tracts (1009)
│ ├── cbf (960)
│ │ ├── arb (728)
│ │ ├── cbc (744)
│ │ └── cbp (752)
│ │ ├── icp (1123)
│ │ │ └── sctd (553)
│ │ ├── mcp (78)
│ │ └── scp (326)
│ │ ├── dscp (812)
│ │ ├── sctv (866)
│ │ └── uf (850)
│ ├── cm (967)
│ │ ├── IIIn (832)
│ │ │ ├── mlf (62)
│ │ │ └── pc (158)
│ │ ├── IIn (848)
│ │ │ ├── bsc (916)
│ │ │ ├── csc (336)
│ │ │ ├── och (117)
│ │ │ └── opt (125)
│ │ ├── IVn (911)
│ │ ├── In (840)
│ │ │ ├── aco (900)
│ │ │ ├── lotg (21)
│ │ │ │ ├── lot (665)
│ │ │ │ └── lotd (538)
│ │ │ └── onl (1016)
│ │ ├── VIIIn (933)
│ │ │ ├── cVIIIn (948)
│ │ │ │ ├── bic (482)
│ │ │ │ ├── cic (633)
│ │ │ │ ├── das (506)
│ │ │ │ ├── ll (658)
│ │ │ │ └── tb (841)
│ │ │ └── vVIIIn (413)
│ │ ├── VIIn (798)
│ │ │ └── gVIIn (1116)
│ │ ├── Vn (901)
│ │ │ ├── moV (93)
│ │ │ └── sV (229)
│ │ │ └── sptV (794)
│ │ ├── Xn (917)
│ │ │ └── ts (237)
│ │ ├── drt (792)
│ │ │ └── cett (932)
│ │ │ ├── dc (514)
│ │ │ │ └── cuf (380)
│ │ │ └── ml (697)
│ │ └── von (949)
│ ├── eps (1000)
│ │ ├── epsc (760)
│ │ │ └── nst (102)
│ │ ├── rust (863)
│ │ │ └── vtd (397)
│ │ └── tsp (877)
│ │ ├── dtd (1060)
│ │ ├── tspc (1043)
│ │ └── tspd (1051)
│ ├── lfbs (983)
│ │ ├── cc (776)
│ │ │ ├── ccb (484682516)
│ │ │ ├── ccg (1108)
│ │ │ ├── ccs (986)
│ │ │ ├── ee (964)
│ │ │ ├── fa (956)
│ │ │ │ └── ec (579)
│ │ │ └── fp (971)
│ │ ├── cst (784)
│ │ │ ├── cpd (924)
│ │ │ ├── int (6)
│ │ │ ├── py (190)
│ │ │ └── pyd (198)
│ │ └── lfbst (896)
│ │ ├── ar (484682524)
│ │ ├── em (1092)
│ │ └── or (484682520)
│ ├── mfbs (991)
│ │ ├── mfbc (768)
│ │ │ ├── act (908)
│ │ │ ├── amc (884)
│ │ │ ├── cing (940)
│ │ │ ├── fxs (1099)
│ │ │ │ ├── alv (466)
│ │ │ │ ├── df (530)
│ │ │ │ ├── fi (603)
│ │ │ │ ├── fxpo (737)
│ │ │ │ │ ├── fx (436)
│ │ │ │ │ └── mct (428)
│ │ │ │ └── hc (618)
│ │ │ │ ├── dhc (443)
│ │ │ │ └── vhc (449)
│ │ │ └── st (301)
│ │ │ └── stc (484682528)
│ │ └── mfsbshy (824)
│ │ ├── mfb (54)
│ │ ├── mfbse (1083)
│ │ │ ├── fr (595)
│ │ │ ├── hbc (611)
│ │ │ └── sm (802)
│ │ ├── mfbsma (46)
│ │ │ ├── mp (673)
│ │ │ ├── mtg (681)
│ │ │ ├── mtt (690)
│ │ │ └── pm (753)
│ │ └── sup (349)
│ └── scwm (484682512)
└── grey (8)
├── BS (343)
│ ├── HB (1065)
│ │ ├── MY (354)
│ │ │ ├── MY-mot (370)
│ │ │ │ ├── ACVII (576)
│ │ │ │ ├── AMB (135)
│ │ │ │ │ ├── AMBd (939)
│ │ │ │ │ └── AMBv (143)
│ │ │ │ ├── DMX (839)
│ │ │ │ ├── GRN (1048)
│ │ │ │ ├── ICB (372)
│ │ │ │ ├── IO (83)
│ │ │ │ ├── IRN (136)
│ │ │ │ ├── ISN (106)
│ │ │ │ ├── LIN (203)
│ │ │ │ ├── LRN (235)
│ │ │ │ │ ├── LRNm (955)
│ │ │ │ │ └── LRNp (963)
│ │ │ │ ├── MARN (307)
│ │ │ │ ├── MDRN (395)
│ │ │ │ │ ├── MDRNd (1098)
│ │ │ │ │ └── MDRNv (1107)
│ │ │ │ ├── PARN (852)
│ │ │ │ ├── PAS (859)
│ │ │ │ ├── PGRN (938)
│ │ │ │ │ ├── PGRNd (970)
│ │ │ │ │ └── PGRNl (978)
│ │ │ │ ├── PHY (154)
│ │ │ │ │ ├── NR (177)
│ │ │ │ │ └── PRP (169)
│ │ │ │ ├── PPY (1069)
│ │ │ │ ├── VI (653)
│ │ │ │ ├── VII (661)
│ │ │ │ ├── VNC (701)
│ │ │ │ │ ├── LAV (209)
│ │ │ │ │ ├── MV (202)
│ │ │ │ │ ├── SPIV (225)
│ │ │ │ │ └── SUV (217)
│ │ │ │ ├── XII (773)
│ │ │ │ ├── x (765)
│ │ │ │ └── y (781)
│ │ │ ├── MY-sat (379)
│ │ │ │ ├── RM (206)
│ │ │ │ ├── RO (222)
│ │ │ │ └── RPA (230)
│ │ │ └── MY-sen (386)
│ │ │ ├── AP (207)
│ │ │ ├── CN (607)
│ │ │ │ ├── DCO (96)
│ │ │ │ └── VCO (101)
│ │ │ ├── DCN (720)
│ │ │ │ ├── CU (711)
│ │ │ │ └── GR (1039)
│ │ │ ├── ECU (903)
│ │ │ ├── NTB (642)
│ │ │ ├── NTS (651)
│ │ │ ├── Pa5 (589508451)
│ │ │ ├── SPVC (429)
│ │ │ ├── SPVI (437)
│ │ │ └── SPVO (445)
│ │ └── P (771)
│ │ ├── P-mot (987)
│ │ │ ├── Acs5 (549009219)
│ │ │ ├── B (280)
│ │ │ ├── DTN (880)
│ │ │ ├── I5 (549009227)
│ │ │ ├── P5 (549009215)
│ │ │ ├── PC5 (549009223)
│ │ │ ├── PCG (898)
│ │ │ ├── PDTg (599626927)
│ │ │ ├── PG (931)
│ │ │ ├── PRNc (1093)
│ │ │ ├── SG (318)
│ │ │ ├── SUT (534)
│ │ │ ├── TRN (574)
│ │ │ └── V (621)
│ │ ├── P-sat (1117)
│ │ │ ├── CS (679)
│ │ │ ├── LC (147)
│ │ │ ├── LDT (162)
│ │ │ ├── NI (604)
│ │ │ ├── PRNr (146)
│ │ │ ├── RPO (238)
│ │ │ ├── SLC (350)
│ │ │ └── SLD (358)
│ │ └── P-sen (1132)
│ │ ├── NLL (612)
│ │ ├── PB (867)
│ │ │ └── KF (123)
│ │ ├── PSV (7)
│ │ └── SOC (398)
│ │ ├── POR (122)
│ │ ├── SOCl (114)
│ │ └── SOCm (105)
│ ├── IB (1129)
│ │ ├── HY (1097)
│ │ │ ├── LZ (290)
│ │ │ │ ├── LHA (194)
│ │ │ │ ├── LPO (226)
│ │ │ │ ├── PST (356)
│ │ │ │ ├── PSTN (364)
│ │ │ │ ├── PeF (576073704)
│ │ │ │ ├── RCH (173)
│ │ │ │ ├── STN (470)
│ │ │ │ ├── TU (614)
│ │ │ │ └── ZI (797)
│ │ │ │ └── FF (804)
│ │ │ ├── ME (10671)
│ │ │ ├── MEZ (467)
│ │ │ │ ├── AHN (88)
│ │ │ │ ├── MBO (331)
│ │ │ │ │ ├── LM (210)
│ │ │ │ │ ├── MM (491)
│ │ │ │ │ │ ├── MMd (606826659)
│ │ │ │ │ │ ├── MMl (606826647)
│ │ │ │ │ │ ├── MMm (606826651)
│ │ │ │ │ │ ├── MMme (732)
│ │ │ │ │ │ └── MMp (606826655)
│ │ │ │ │ ├── SUM (525)
│ │ │ │ │ └── TM (557)
│ │ │ │ │ ├── TMd (1126)
│ │ │ │ │ └── TMv (1)
│ │ │ │ ├── MPN (515)
│ │ │ │ ├── PH (946)
│ │ │ │ ├── PMd (980)
│ │ │ │ ├── PMv (1004)
│ │ │ │ ├── PVHd (63)
│ │ │ │ └── VMH (693)
│ │ │ ├── PVR (141)
│ │ │ │ ├── ADP (72)
│ │ │ │ ├── AVP (263)
│ │ │ │ ├── AVPV (272)
│ │ │ │ ├── DMH (830)
│ │ │ │ ├── MEPO (452)
│ │ │ │ ├── MPO (523)
│ │ │ │ ├── OV (763)
│ │ │ │ ├── PD (914)
│ │ │ │ ├── PS (1109)
│ │ │ │ ├── PVp (126)
│ │ │ │ ├── PVpo (133)
│ │ │ │ ├── SBPV (347)
│ │ │ │ ├── SCH (286)
│ │ │ │ ├── SFO (338)
│ │ │ │ ├── VLPO (689)
│ │ │ │ └── VMPO (576073699)
│ │ │ └── PVZ (157)
│ │ │ ├── ARH (223)
│ │ │ ├── ASO (332)
│ │ │ ├── PVH (38)
│ │ │ ├── PVa (30)
│ │ │ ├── PVi (118)
│ │ │ └── SO (390)
│ │ └── TH (549)
│ │ ├── DORpm (856)
│ │ │ ├── ATN (239)
│ │ │ │ ├── AD (64)
│ │ │ │ ├── AM (127)
│ │ │ │ │ ├── AMd (1096)
│ │ │ │ │ └── AMv (1104)
│ │ │ │ ├── AV (255)
│ │ │ │ ├── IAD (1113)
│ │ │ │ ├── IAM (1120)
│ │ │ │ └── LD (155)
│ │ │ ├── EPI (958)
│ │ │ │ ├── LH (186)
│ │ │ │ └── MH (483)
│ │ │ ├── GENv (1014)
│ │ │ │ ├── IGL (27)
│ │ │ │ ├── IntG (563807439)
│ │ │ │ ├── LGv (178)
│ │ │ │ └── SubG (321)
│ │ │ ├── ILM (51)
│ │ │ │ ├── CL (575)
│ │ │ │ ├── CM (599)
│ │ │ │ ├── PCN (907)
│ │ │ │ ├── PF (930)
│ │ │ │ ├── PIL (560581563)
│ │ │ │ └── RH (189)
│ │ │ ├── LAT (138)
│ │ │ │ ├── Eth (560581551)
│ │ │ │ ├── LP (218)
│ │ │ │ ├── PO (1020)
│ │ │ │ ├── POL (1029)
│ │ │ │ └── SGN (325)
│ │ │ ├── MED (444)
│ │ │ │ ├── IMD (59)
│ │ │ │ ├── MD (362)
│ │ │ │ ├── PR (1077)
│ │ │ │ └── SMT (366)
│ │ │ ├── MTN (571)
│ │ │ │ ├── PT (15)
│ │ │ │ ├── PVT (149)
│ │ │ │ ├── RE (181)
│ │ │ │ └── Xi (560581559)
│ │ │ └── RT (262)
│ │ └── DORsm (864)
│ │ ├── GENd (1008)
│ │ │ ├── LGd (170)
│ │ │ │ ├── LGd-co (496345668)
│ │ │ │ ├── LGd-ip (496345672)
│ │ │ │ └── LGd-sh (496345664)
│ │ │ └── MG (475)
│ │ │ ├── MGd (1072)
│ │ │ ├── MGm (1088)
│ │ │ └── MGv (1079)
│ │ ├── PP (1044)
│ │ ├── SPA (609)
│ │ ├── SPF (406)
│ │ │ ├── SPFm (414)
│ │ │ └── SPFp (422)
│ │ └── VENT (637)
│ │ ├── PoT (563807435)
│ │ ├── VAL (629)
│ │ ├── VM (685)
│ │ └── VP (709)
│ │ ├── VPL (718)
│ │ ├── VPLpc (725)
│ │ ├── VPM (733)
│ │ └── VPMpc (741)
│ └── MB (313)
│ ├── MBmot (323)
│ │ ├── AT (231)
│ │ ├── CUN (616)
│ │ ├── DT (75)
│ │ ├── EW (975)
│ │ ├── III (35)
│ │ ├── IV (115)
│ │ ├── LT (66)
│ │ ├── MA3 (549009211)
│ │ ├── MRN (128)
│ │ ├── MT (58)
│ │ ├── PAG (795)
│ │ │ ├── INC (67)
│ │ │ ├── ND (587)
│ │ │ ├── PRC (50)
│ │ │ └── Su3 (614454277)
│ │ ├── PN (607344830)
│ │ ├── PRT (1100)
│ │ │ ├── APN (215)
│ │ │ ├── MPT (531)
│ │ │ ├── NOT (628)
│ │ │ ├── NPC (634)
│ │ │ ├── OP (706)
│ │ │ ├── PPT (1061)
│ │ │ └── RPF (549009203)
│ │ ├── Pa4 (606826663)
│ │ ├── RN (214)
│ │ ├── RR (246)
│ │ ├── SCm (294)
│ │ │ ├── SCdg (26)
│ │ │ ├── SCdw (42)
│ │ │ ├── SCig (10)
│ │ │ └── SCiw (17)
│ │ ├── SNr (381)
│ │ ├── VTA (749)
│ │ └── VTN (757)
│ ├── MBsen (339)
│ │ ├── IC (4)
│ │ │ ├── ICc (811)
│ │ │ ├── ICd (820)
│ │ │ └── ICe (828)
│ │ ├── MEV (460)
│ │ ├── NB (580)
│ │ ├── PBG (874)
│ │ ├── SAG (271)
│ │ ├── SCO (599626923)
│ │ └── SCs (302)
│ │ ├── SCop (851)
│ │ ├── SCsg (842)
│ │ └── SCzo (834)
│ └── MBsta (348)
│ ├── PPN (1052)
│ ├── RAmb (165)
│ │ ├── CLI (591)
│ │ ├── DR (872)
│ │ ├── IF (12)
│ │ ├── IPN (100)
│ │ │ ├── IPA (607344842)
│ │ │ ├── IPC (607344838)
│ │ │ ├── IPDL (607344858)
│ │ │ ├── IPDM (607344854)
│ │ │ ├── IPI (607344850)
│ │ │ ├── IPL (607344846)
│ │ │ ├── IPR (607344834)
│ │ │ └── IPRL (607344862)
│ │ └── RL (197)
│ └── SNc (374)
├── CB (512)
│ ├── CBN (519)
│ │ ├── DN (846)
│ │ ├── FN (989)
│ │ ├── IP (91)
│ │ └── VeCB (589508455)
│ └── CBX (528)
│ ├── HEM (1073)
│ │ ├── AN (1017)
│ │ │ ├── ANcr1 (1056)
│ │ │ └── ANcr2 (1064)
│ │ ├── COPY (1033)
│ │ ├── FL (1049)
│ │ ├── PFL (1041)
│ │ ├── PRM (1025)
│ │ └── SIM (1007)
│ └── VERM (645)
│ ├── CENT (920)
│ │ ├── CENT2 (976)
│ │ └── CENT3 (984)
│ ├── CUL (928)
│ │ └── CUL4, 5 (1091)
│ ├── DEC (936)
│ ├── FOTU (944)
│ ├── LING (912)
│ ├── NOD (968)
│ ├── PYR (951)
│ └── UVU (957)
└── CH (567)
├── CNU (623)
│ ├── PAL (803)
│ │ ├── PALc (809)
│ │ │ ├── BAC (287)
│ │ │ └── BST (351)
│ │ ├── PALd (818)
│ │ │ ├── GPe (1022)
│ │ │ └── GPi (1031)
│ │ ├── PALm (826)
│ │ │ ├── MSC (904)
│ │ │ │ ├── MS (564)
│ │ │ │ └── NDB (596)
│ │ │ └── TRS (581)
│ │ └── PALv (835)
│ │ ├── MA (298)
│ │ └── SI (342)
│ └── STR (477)
│ ├── LSX (275)
│ │ ├── LS (242)
│ │ │ ├── LSc (250)
│ │ │ ├── LSr (258)
│ │ │ └── LSv (266)
│ │ ├── SF (310)
│ │ └── SH (333)
│ ├── STRd (485)
│ │ └── CP (672)
│ ├── STRv (493)
│ │ ├── ACB (56)
│ │ ├── FS (998)
│ │ └── OT (754)
│ └── sAMY (278)
│ ├── AAA (23)
│ ├── BA (292)
│ ├── CEA (536)
│ │ ├── CEAc (544)
│ │ ├── CEAl (551)
│ │ └── CEAm (559)
│ ├── IA (1105)
│ └── MEA (403)
└── CTX (688)
├── CTXpl (695)
│ ├── HPF (1089)
│ │ ├── HIP (1080)
│ │ │ ├── CA (375)
│ │ │ │ ├── CA1 (382)
│ │ │ │ ├── CA2 (423)
│ │ │ │ └── CA3 (463)
│ │ │ ├── DG (726)
│ │ │ │ ├── DG-mo (10703)
│ │ │ │ ├── DG-po (10704)
│ │ │ │ └── DG-sg (632)
│ │ │ ├── FC (982)
│ │ │ └── IG (19)
│ │ └── RHP (822)
│ │ ├── APr (484682508)
│ │ ├── ENT (909)
│ │ │ ├── ENTl (918)
│ │ │ │ ├── ENTl1 (1121)
│ │ │ │ ├── ENTl2 (20)
│ │ │ │ ├── ENTl3 (52)
│ │ │ │ ├── ENTl5 (139)
│ │ │ │ └── ENTl6a (28)
│ │ │ └── ENTm (926)
│ │ │ ├── ENTm1 (526)
│ │ │ ├── ENTm2 (543)
│ │ │ ├── ENTm3 (664)
│ │ │ ├── ENTm5 (727)
│ │ │ └── ENTm6 (743)
│ │ ├── HATA (589508447)
│ │ ├── PAR (843)
│ │ ├── POST (1037)
│ │ ├── PRE (1084)
│ │ ├── ProS (484682470)
│ │ └── SUB (502)
│ ├── Isocortex (315)
│ │ ├── ACA (31)
│ │ │ ├── ACAd (39)
│ │ │ │ ├── ACAd1 (935)
│ │ │ │ ├── ACAd2/3 (211)
│ │ │ │ ├── ACAd5 (1015)
│ │ │ │ ├── ACAd6a (919)
│ │ │ │ └── ACAd6b (927)
│ │ │ └── ACAv (48)
│ │ │ ├── ACAv1 (588)
│ │ │ ├── ACAv2/3 (296)
│ │ │ ├── ACAv5 (772)
│ │ │ ├── ACAv6a (810)
│ │ │ └── ACAv6b (819)
│ │ ├── AI (95)
│ │ │ ├── AId (104)
│ │ │ │ ├── AId1 (996)
│ │ │ │ ├── AId2/3 (328)
│ │ │ │ ├── AId5 (1101)
│ │ │ │ ├── AId6a (783)
│ │ │ │ └── AId6b (831)
│ │ │ ├── AIp (111)
│ │ │ │ ├── AIp1 (120)
│ │ │ │ ├── AIp2/3 (163)
│ │ │ │ ├── AIp5 (344)
│ │ │ │ ├── AIp6a (314)
│ │ │ │ └── AIp6b (355)
│ │ │ └── AIv (119)
│ │ │ ├── AIv1 (704)
│ │ │ ├── AIv2/3 (694)
│ │ │ ├── AIv5 (800)
│ │ │ ├── AIv6a (675)
│ │ │ └── AIv6b (699)
│ │ ├── AUD (247)
│ │ │ ├── AUDd (1011)
│ │ │ │ ├── AUDd1 (527)
│ │ │ │ ├── AUDd2/3 (600)
│ │ │ │ ├── AUDd4 (678)
│ │ │ │ ├── AUDd5 (252)
│ │ │ │ ├── AUDd6a (156)
│ │ │ │ └── AUDd6b (243)
│ │ │ ├── AUDp (1002)
│ │ │ │ ├── AUDp1 (735)
│ │ │ │ ├── AUDp2/3 (251)
│ │ │ │ ├── AUDp4 (816)
│ │ │ │ ├── AUDp5 (847)
│ │ │ │ ├── AUDp6a (954)
│ │ │ │ └── AUDp6b (1005)
│ │ │ ├── AUDpo (1027)
│ │ │ │ ├── AUDpo1 (696)
│ │ │ │ ├── AUDpo2/3 (643)
│ │ │ │ ├── AUDpo4 (759)
│ │ │ │ ├── AUDpo5 (791)
│ │ │ │ ├── AUDpo6a (249)
│ │ │ │ └── AUDpo6b (456)
│ │ │ └── AUDv (1018)
│ │ │ ├── AUDv1 (959)
│ │ │ ├── AUDv2/3 (755)
│ │ │ ├── AUDv4 (990)
│ │ │ ├── AUDv5 (1023)
│ │ │ ├── AUDv6a (520)
│ │ │ └── AUDv6b (598)
│ │ ├── ECT (895)
│ │ │ ├── ECT1 (836)
│ │ │ ├── ECT2/3 (427)
│ │ │ ├── ECT5 (988)
│ │ │ ├── ECT6a (977)
│ │ │ └── ECT6b (1045)
│ │ ├── FRP (184)
│ │ │ ├── FRP1 (68)
│ │ │ ├── FRP2/3 (667)
│ │ │ ├── FRP5 (526157192)
│ │ │ ├── FRP6a (526157196)
│ │ │ └── FRP6b (526322264)
│ │ ├── GU (1057)
│ │ │ ├── GU1 (36)
│ │ │ ├── GU2/3 (180)
│ │ │ ├── GU4 (148)
│ │ │ ├── GU5 (187)
│ │ │ ├── GU6a (638)
│ │ │ └── GU6b (662)
│ │ ├── ILA (44)
│ │ │ ├── ILA1 (707)
│ │ │ ├── ILA2/3 (556)
│ │ │ ├── ILA5 (827)
│ │ │ ├── ILA6a (1054)
│ │ │ └── ILA6b (1081)
│ │ ├── MO (500)
│ │ │ ├── MOp (985)
│ │ │ │ ├── MOp1 (320)
│ │ │ │ ├── MOp2/3 (943)
│ │ │ │ ├── MOp5 (648)
│ │ │ │ ├── MOp6a (844)
│ │ │ │ └── MOp6b (882)
│ │ │ └── MOs (993)
│ │ │ ├── MOs1 (656)
│ │ │ ├── MOs2/3 (962)
│ │ │ ├── MOs5 (767)
│ │ │ ├── MOs6a (1021)
│ │ │ └── MOs6b (1085)
│ │ ├── ORB (714)
│ │ │ ├── ORBl (723)
│ │ │ │ ├── ORBl1 (448)
│ │ │ │ ├── ORBl2/3 (412)
│ │ │ │ ├── ORBl5 (630)
│ │ │ │ ├── ORBl6a (440)
│ │ │ │ └── ORBl6b (488)
│ │ │ ├── ORBm (731)
│ │ │ │ ├── ORBm1 (484)
│ │ │ │ ├── ORBm2/3 (582)
│ │ │ │ ├── ORBm5 (620)
│ │ │ │ ├── ORBm6a (910)
│ │ │ │ └── ORBm6b (527696977)
│ │ │ └── ORBvl (746)
│ │ │ ├── ORBvl1 (969)
│ │ │ ├── ORBvl2/3 (288)
│ │ │ ├── ORBvl5 (1125)
│ │ │ ├── ORBvl6a (608)
│ │ │ └── ORBvl6b (680)
│ │ ├── PERI (922)
│ │ │ ├── PERI1 (540)
│ │ │ ├── PERI2/3 (888)
│ │ │ ├── PERI5 (692)
│ │ │ ├── PERI6a (335)
│ │ │ └── PERI6b (368)
│ │ ├── PL (972)
│ │ │ ├── PL1 (171)
│ │ │ ├── PL2/3 (304)
│ │ │ ├── PL5 (363)
│ │ │ ├── PL6a (84)
│ │ │ └── PL6b (132)
│ │ ├── PTLp (22)
│ │ │ ├── VISa (312782546)
│ │ │ │ ├── VISa1 (312782550)
│ │ │ │ ├── VISa2/3 (312782554)
│ │ │ │ ├── VISa4 (312782558)
│ │ │ │ ├── VISa5 (312782562)
│ │ │ │ ├── VISa6a (312782566)
│ │ │ │ └── VISa6b (312782570)
│ │ │ └── VISrl (417)
│ │ │ ├── VISrl1 (312782604)
│ │ │ ├── VISrl2/3 (312782608)
│ │ │ ├── VISrl4 (312782612)
│ │ │ ├── VISrl5 (312782616)
│ │ │ ├── VISrl6a (312782620)
│ │ │ └── VISrl6b (312782624)
│ │ ├── RSP (254)
│ │ │ ├── RSPagl (894)
│ │ │ │ ├── RSPagl1 (671)
│ │ │ │ ├── RSPagl2/3 (965)
│ │ │ │ ├── RSPagl5 (774)
│ │ │ │ ├── RSPagl6a (906)
│ │ │ │ └── RSPagl6b (279)
│ │ │ ├── RSPd (879)
│ │ │ │ ├── RSPd1 (442)
│ │ │ │ ├── RSPd2/3 (434)
│ │ │ │ ├── RSPd4 (545)
│ │ │ │ ├── RSPd5 (610)
│ │ │ │ ├── RSPd6a (274)
│ │ │ │ └── RSPd6b (330)
│ │ │ └── RSPv (886)
│ │ │ ├── RSPv1 (542)
│ │ │ ├── RSPv2/3 (430)
│ │ │ ├── RSPv5 (687)
│ │ │ ├── RSPv6a (590)
│ │ │ └── RSPv6b (622)
│ │ ├── SS (453)
│ │ │ ├── SSp (322)
│ │ │ │ ├── SSp-bfd (329)
│ │ │ │ │ ├── SSp-bfd1 (981)
│ │ │ │ │ ├── SSp-bfd2/3 (201)
│ │ │ │ │ ├── SSp-bfd4 (1047)
│ │ │ │ │ ├── SSp-bfd5 (1070)
│ │ │ │ │ ├── SSp-bfd6a (1038)
│ │ │ │ │ └── SSp-bfd6b (1062)
│ │ │ │ ├── SSp-ll (337)
│ │ │ │ │ ├── SSp-ll1 (1030)
│ │ │ │ │ ├── SSp-ll2/3 (113)
│ │ │ │ │ ├── SSp-ll4 (1094)
│ │ │ │ │ ├── SSp-ll5 (1128)
│ │ │ │ │ ├── SSp-ll6a (478)
│ │ │ │ │ └── SSp-ll6b (510)
│ │ │ │ ├── SSp-m (345)
│ │ │ │ │ ├── SSp-m1 (878)
│ │ │ │ │ ├── SSp-m2/3 (657)
│ │ │ │ │ ├── SSp-m4 (950)
│ │ │ │ │ ├── SSp-m5 (974)
│ │ │ │ │ ├── SSp-m6a (1102)
│ │ │ │ │ └── SSp-m6b (2)
│ │ │ │ ├── SSp-n (353)
│ │ │ │ │ ├── SSp-n1 (558)
│ │ │ │ │ ├── SSp-n2/3 (838)
│ │ │ │ │ ├── SSp-n4 (654)
│ │ │ │ │ ├── SSp-n5 (702)
│ │ │ │ │ ├── SSp-n6a (889)
│ │ │ │ │ └── SSp-n6b (929)
│ │ │ │ ├── SSp-tr (361)
│ │ │ │ │ ├── SSp-tr1 (1006)
│ │ │ │ │ ├── SSp-tr2/3 (670)
│ │ │ │ │ ├── SSp-tr4 (1086)
│ │ │ │ │ ├── SSp-tr5 (1111)
│ │ │ │ │ ├── SSp-tr6a (9)
│ │ │ │ │ └── SSp-tr6b (461)
│ │ │ │ ├── SSp-ul (369)
│ │ │ │ │ ├── SSp-ul1 (450)
│ │ │ │ │ ├── SSp-ul2/3 (854)
│ │ │ │ │ ├── SSp-ul4 (577)
│ │ │ │ │ ├── SSp-ul5 (625)
│ │ │ │ │ ├── SSp-ul6a (945)
│ │ │ │ │ └── SSp-ul6b (1026)
│ │ │ │ └── SSp-un (182305689)
│ │ │ │ ├── SSp-un1 (182305693)
│ │ │ │ ├── SSp-un2/3 (182305697)
│ │ │ │ ├── SSp-un4 (182305701)
│ │ │ │ ├── SSp-un5 (182305705)
│ │ │ │ ├── SSp-un6a (182305709)
│ │ │ │ └── SSp-un6b (182305713)
│ │ │ └── SSs (378)
│ │ │ ├── SSs1 (873)
│ │ │ ├── SSs2/3 (806)
│ │ │ ├── SSs4 (1035)
│ │ │ ├── SSs5 (1090)
│ │ │ ├── SSs6a (862)
│ │ │ └── SSs6b (893)
│ │ ├── TEa (541)
│ │ │ ├── TEa1 (97)
│ │ │ ├── TEa2/3 (1127)
│ │ │ ├── TEa4 (234)
│ │ │ ├── TEa5 (289)
│ │ │ ├── TEa6a (729)
│ │ │ └── TEa6b (786)
│ │ ├── VIS (669)
│ │ │ ├── VISal (402)
│ │ │ │ ├── VISal1 (1074)
│ │ │ │ ├── VISal2/3 (905)
│ │ │ │ ├── VISal4 (1114)
│ │ │ │ ├── VISal5 (233)
│ │ │ │ ├── VISal6a (601)
│ │ │ │ └── VISal6b (649)
│ │ │ ├── VISam (394)
│ │ │ │ ├── VISam1 (281)
│ │ │ │ ├── VISam2/3 (1066)
│ │ │ │ ├── VISam4 (401)
│ │ │ │ ├── VISam5 (433)
│ │ │ │ ├── VISam6a (1046)
│ │ │ │ └── VISam6b (441)
│ │ │ ├── VISl (409)
│ │ │ │ ├── VISl1 (421)
│ │ │ │ ├── VISl2/3 (973)
│ │ │ │ ├── VISl4 (573)
│ │ │ │ ├── VISl5 (613)
│ │ │ │ ├── VISl6a (74)
│ │ │ │ └── VISl6b (121)
│ │ │ ├── VISli (312782574)
│ │ │ │ ├── VISli1 (312782578)
│ │ │ │ ├── VISli2/3 (312782582)
│ │ │ │ ├── VISli4 (312782586)
│ │ │ │ ├── VISli5 (312782590)
│ │ │ │ ├── VISli6a (312782594)
│ │ │ │ └── VISli6b (312782598)
│ │ │ ├── VISp (385)
│ │ │ │ ├── VISp1 (593)
│ │ │ │ ├── VISp2/3 (821)
│ │ │ │ ├── VISp4 (721)
│ │ │ │ ├── VISp5 (778)
│ │ │ │ ├── VISp6a (33)
│ │ │ │ └── VISp6b (305)
│ │ │ ├── VISpl (425)
│ │ │ │ ├── VISpl1 (750)
│ │ │ │ ├── VISpl2/3 (269)
│ │ │ │ ├── VISpl4 (869)
│ │ │ │ ├── VISpl5 (902)
│ │ │ │ ├── VISpl6a (377)
│ │ │ │ └── VISpl6b (393)
│ │ │ ├── VISpm (533)
│ │ │ │ ├── VISpm1 (805)
│ │ │ │ ├── VISpm2/3 (41)
│ │ │ │ ├── VISpm4 (501)
│ │ │ │ ├── VISpm5 (565)
│ │ │ │ ├── VISpm6a (257)
│ │ │ │ └── VISpm6b (469)
│ │ │ └── VISpor (312782628)
│ │ │ ├── VISpor1 (312782632)
│ │ │ ├── VISpor2/3 (312782636)
│ │ │ ├── VISpor4 (312782640)
│ │ │ ├── VISpor5 (312782644)
│ │ │ ├── VISpor6a (312782648)
│ │ │ └── VISpor6b (312782652)
│ │ └── VISC (677)
│ │ ├── VISC1 (897)
│ │ ├── VISC2/3 (1106)
│ │ ├── VISC4 (1010)
│ │ ├── VISC5 (1058)
│ │ ├── VISC6a (857)
│ │ └── VISC6b (849)
│ └── OLF (698)
│ ├── AOB (151)
│ │ ├── AOBgl (188)
│ │ ├── AOBgr (196)
│ │ └── AOBmi (204)
│ ├── AON (159)
│ ├── COA (631)
│ │ ├── COAa (639)
│ │ └── COAp (647)
│ │ ├── COApl (655)
│ │ └── COApm (663)
│ ├── DP (814)
│ ├── MOB (507)
│ ├── NLOT (619)
│ │ ├── NLOT1 (260)
│ │ ├── NLOT2 (268)
│ │ └── NLOT3 (1139)
│ ├── PAA (788)
│ ├── PIR (961)
│ ├── TR (566)
│ └── TT (589)
│ ├── TTd (597)
│ └── TTv (605)
└── CTXsp (703)
├── BLA (295)
│ ├── BLAa (303)
│ ├── BLAp (311)
│ └── BLAv (451)
├── BMA (319)
│ ├── BMAa (327)
│ └── BMAp (334)
├── CLA (583)
├── EP (942)
│ ├── EPd (952)
│ └── EPv (966)
├── LA (131)
└── PA (780)
