Receptive fields#
Tutorial overview#
One of the most important features of visually responsive neurons is the location and extent of their receptive field. Is it highly localized or spatially distributed? Is it centered on the stimulus display, or is it on an edge? How much does it overlap with the receptive fields of neurons in other regions? Obtaining answers to these questions is a crucial step for interpreting a results related to neurons’ visual coding properties.
This Jupyter notebook will cover the following topics:
Understanding the receptive field stimulus used in the Neuropixels Visual Coding experiments
Obtaining pre-computed metrics related to receptive fields (coming soon)
Finding experiments of interest based on receptive field overlap (coming soon)
This tutorial assumes you’ve already created a data cache, or are working with the files on AWS. If you haven’t reached that step yet, we recommend going through the data access tutorial first.
Functions related to additional aspects of data analysis will be covered in other tutorials. For a full list of available tutorials, see the Visual Coding page.
Let’s start by creating an EcephysProjectCache object, and pointing it to a
new or existing manifest file:
import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
from allensdk.brain_observatory.ecephys.ecephys_project_cache import EcephysProjectCache
/opt/envs/allensdk/lib/python3.10/site-packages/tqdm/auto.py:21: TqdmWarning: IProgress not found. Please update jupyter and ipywidgets. See https://ipywidgets.readthedocs.io/en/stable/user_install.html
from .autonotebook import tqdm as notebook_tqdm
If you’re not sure what a manifest file is or where to put it, please check out data access tutorial before going further.
# Example cache directory path, it determines where downloaded data will be stored
output_dir = '/root/capsule/data/allen-brain-observatory/visual-coding-neuropixels/ecephys-cache/'
manifest_path = os.path.join(output_dir, "manifest.json")
cache = EcephysProjectCache.from_warehouse(manifest=manifest_path)
Let’s load the sessions table and grab the data for one experiment in the list:
sessions = cache.get_session_table()
session_id = 759883607 # An example session id
session = cache.get_session_data(session_id)
/opt/envs/allensdk/lib/python3.10/site-packages/hdmf/utils.py:668: UserWarning: Ignoring cached namespace 'hdmf-common' version 1.1.3 because version 1.8.0 is already loaded.
return func(args[0], **pargs)
/opt/envs/allensdk/lib/python3.10/site-packages/hdmf/utils.py:668: UserWarning: Ignoring cached namespace 'core' version 2.2.2 because version 2.7.0 is already loaded.
return func(args[0], **pargs)
Finding stimuli in session#
In the Visual Coding dataset, a variety of visual stimuli were presented
throughout the recording session. The session object contains all of the spike
data for one recording session, as well as information about the stimulus, mouse
behavior, and probes.
session.stimulus_names
['spontaneous',
'gabors',
'flashes',
'drifting_gratings',
'natural_movie_three',
'natural_movie_one',
'static_gratings',
'natural_scenes']
Stimulus epochs#
These stimuli are interleaved throughout the session. We can use the
stimulus_epochs to see when each stimulus type was presented.
stimulus_epochs = session.get_stimulus_epochs()
stimulus_epochs
| start_time | stop_time | duration | stimulus_name | stimulus_block | |
|---|---|---|---|---|---|
| 0 | 24.737569 | 84.804349 | 60.066780 | spontaneous | null |
| 1 | 84.804349 | 996.849568 | 912.045219 | gabors | 0.0 |
| 2 | 996.849568 | 1285.841049 | 288.991481 | spontaneous | null |
| 3 | 1285.841049 | 1584.340430 | 298.499381 | flashes | 1.0 |
| 4 | 1584.340430 | 1586.091909 | 1.751479 | spontaneous | null |
| 5 | 1586.091909 | 2185.609422 | 599.517513 | drifting_gratings | 2.0 |
| 6 | 2185.609422 | 2216.635329 | 31.025907 | spontaneous | null |
| 7 | 2216.635329 | 2817.137049 | 600.501720 | natural_movie_three | 3.0 |
| 8 | 2817.137049 | 2847.162109 | 30.025060 | spontaneous | null |
| 9 | 2847.162109 | 3147.412999 | 300.250890 | natural_movie_one | 4.0 |
| 10 | 3147.412999 | 3177.438049 | 30.025050 | spontaneous | null |
| 11 | 3177.438049 | 3776.938972 | 599.500923 | drifting_gratings | 5.0 |
| 12 | 3776.938972 | 4078.190639 | 301.251667 | spontaneous | null |
| 13 | 4078.190639 | 4678.692349 | 600.501710 | natural_movie_three | 6.0 |
| 14 | 4678.692349 | 4708.717429 | 30.025080 | spontaneous | null |
| 15 | 4708.717429 | 5398.293582 | 689.576153 | drifting_gratings | 7.0 |
| 16 | 5398.293582 | 5399.294419 | 1.000837 | spontaneous | null |
| 17 | 5399.294419 | 5879.695809 | 480.401390 | static_gratings | 8.0 |
| 18 | 5879.695809 | 5909.720859 | 30.025050 | spontaneous | null |
| 19 | 5909.720859 | 6390.122219 | 480.401360 | natural_scenes | 9.0 |
| 20 | 6390.122219 | 6690.373069 | 300.250850 | spontaneous | null |
| 21 | 6690.373069 | 7170.774439 | 480.401370 | natural_scenes | 10.0 |
| 22 | 7170.774439 | 7200.799529 | 30.025090 | spontaneous | null |
| 23 | 7200.799529 | 7681.234219 | 480.434690 | static_gratings | 11.0 |
| 24 | 7681.234219 | 7711.259299 | 30.025080 | spontaneous | null |
| 25 | 7711.259299 | 8011.510139 | 300.250840 | natural_movie_one | 12.0 |
| 26 | 8011.510139 | 8041.535259 | 30.025120 | spontaneous | null |
| 27 | 8041.535259 | 8569.476330 | 527.941071 | natural_scenes | 13.0 |
| 28 | 8569.476330 | 8612.011859 | 42.535529 | spontaneous | null |
| 29 | 8612.011859 | 9152.463399 | 540.451540 | static_gratings | 14.0 |
We’ll plot of V1 activity with this stimulus epoch information by shading each stimulus with a unique color. The plt.axvspan() is a useful function for this.
spike_times = session.spike_times
max_spike_time = np.fromiter(map(max, spike_times.values()), dtype=np.double).max()
numbins = int(np.ceil(max_spike_time))
v1_units = session.units[session.units.ecephys_structure_acronym=='VISp']
numunits = min(len(v1_units), 50)
v1_binned = np.empty((numunits, numbins))
for i in range(numunits):
unit_id = v1_units.index[i]
spikes = spike_times[unit_id]
for j in range(numbins):
v1_binned[i,j] = len(spikes[(spikes>j)&(spikes<j+1)])
plt.figure(figsize=(20,10))
for i in range(numunits):
plt.plot(i+(v1_binned[i,:]/30.), color='gray')
colors = ['blue','orange','green','red','yellow','purple','magenta','gray','lightblue']
for c, stim_name in enumerate(session.stimulus_names):
stim = stimulus_epochs[stimulus_epochs.stimulus_name==stim_name]
for j in range(len(stim)):
plt.axvspan(xmin=stim["start_time"].iloc[j], xmax=stim["stop_time"].iloc[j], color=colors[c], alpha=0.1)
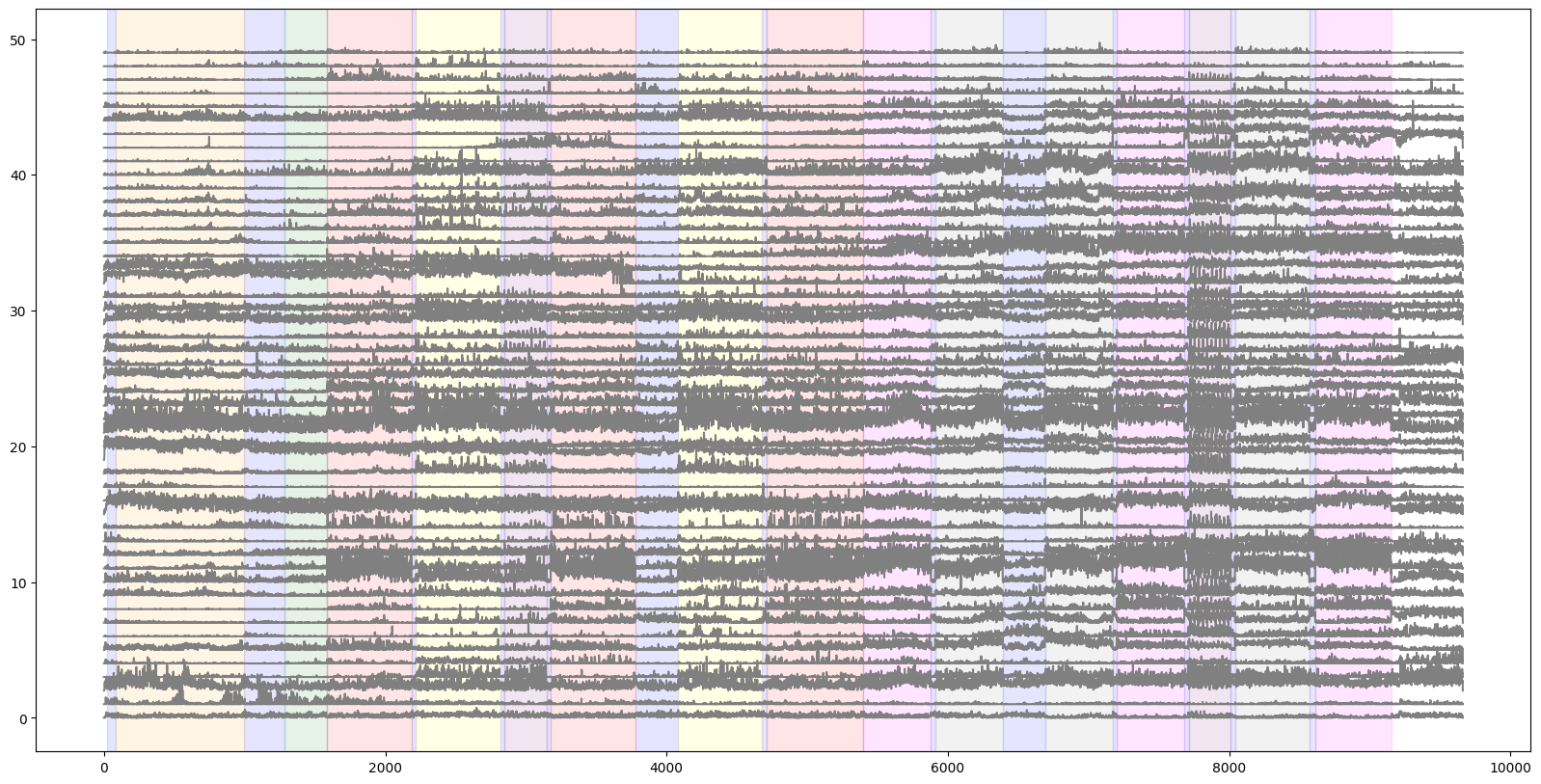
Running speed#
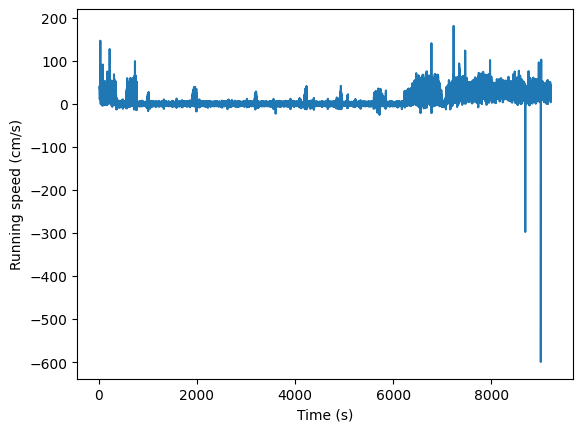
Before we dig further into the stimulus information in more detail, let’s add one more piece of session-wide data to our plot. The mouse’s running speed.
Get the running_speed and its time stamps from the session object. Plot the
speed as a function of time.
plt.plot(session.running_speed.end_time, session.running_speed.velocity)
plt.xlabel("Time (s)")
plt.ylabel("Running speed (cm/s)")
Text(0, 0.5, 'Running speed (cm/s)')
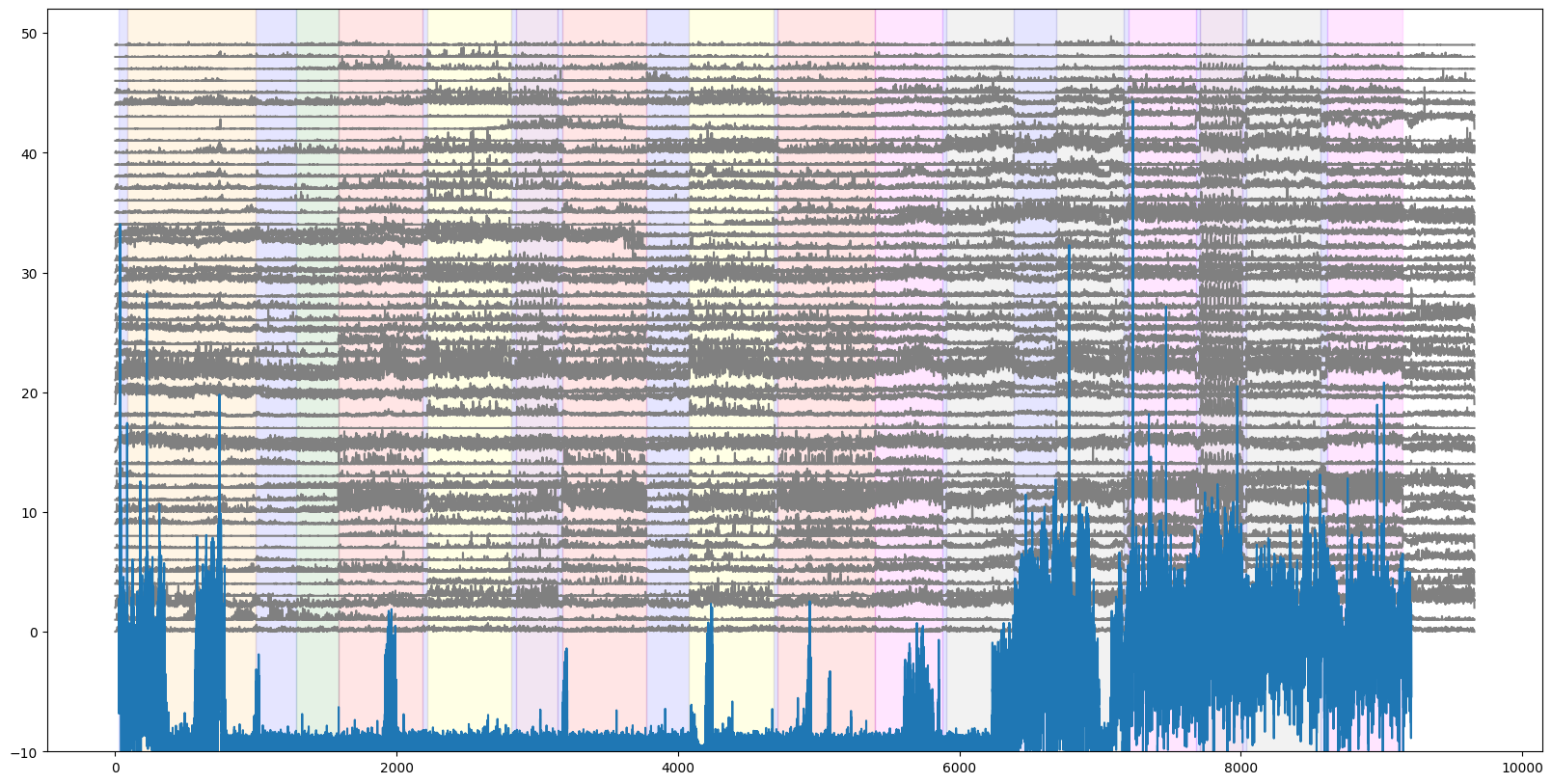
Add the running speed to the plot of V1 activity and stimulus epochs.
plt.figure(figsize=(20,10))
for i in range(numunits):
plt.plot(i+(v1_binned[i,:]/30.), color='gray')
#scale the running speed and offset it on the plot
plt.plot(session.running_speed.end_time, (0.3*session.running_speed.velocity)-10)
colors = ['blue','orange','green','red','yellow','purple','magenta','gray','lightblue']
for c, stim_name in enumerate(session.stimulus_names):
stim = stimulus_epochs[stimulus_epochs.stimulus_name==stim_name]
for j in range(len(stim)):
plt.axvspan(xmin=stim["start_time"].iloc[j], xmax=stim["stop_time"].iloc[j], color=colors[c], alpha=0.1)
plt.ylim(-10,52)
(-10.0, 52.0)
Stimulus presentations#
Now let’s go back and learn more about the stimulus that was presented. The
session object has a function that returns a table for a given stimulus called
get_stimulus_table.
Use this to get the stimulus table for drifting gratings and for natural scenes.
stim_table = session.get_stimulus_table(['drifting_gratings'])
stim_table.head()
| stimulus_block | start_time | stop_time | phase | spatial_frequency | temporal_frequency | stimulus_name | contrast | orientation | size | duration | stimulus_condition_id | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| stimulus_presentation_id | ||||||||||||
| 3798 | 2.0 | 1586.091909 | 1588.093549 | [5308.98333333, 5308.98333333] | 0.04 | 4.0 | drifting_gratings | 0.8 | 270.0 | [250.0, 250.0] | 2.00164 | 246 |
| 3799 | 2.0 | 1589.094372 | 1591.096042 | [5308.98333333, 5308.98333333] | 0.04 | 4.0 | drifting_gratings | 0.8 | 135.0 | [250.0, 250.0] | 2.00167 | 247 |
| 3800 | 2.0 | 1592.096899 | 1594.098559 | [5308.98333333, 5308.98333333] | 0.04 | 8.0 | drifting_gratings | 0.8 | 180.0 | [250.0, 250.0] | 2.00166 | 248 |
| 3801 | 2.0 | 1595.099402 | 1597.101072 | [5308.98333333, 5308.98333333] | 0.04 | 4.0 | drifting_gratings | 0.8 | 270.0 | [250.0, 250.0] | 2.00167 | 246 |
| 3802 | 2.0 | 1598.101909 | 1600.103579 | [5308.98333333, 5308.98333333] | 0.04 | 1.0 | drifting_gratings | 0.8 | 180.0 | [250.0, 250.0] | 2.00167 | 249 |
Now get the stimulus table for natural scenes.
stim_table_ns = session.get_stimulus_table(['natural_scenes'])
stim_table_ns.head()
| stimulus_block | start_time | stop_time | stimulus_name | frame | duration | stimulus_condition_id | |
|---|---|---|---|---|---|---|---|
| stimulus_presentation_id | |||||||
| 51355 | 9.0 | 5909.720859 | 5909.971070 | natural_scenes | 92.0 | 0.250211 | 4908 |
| 51356 | 9.0 | 5909.971070 | 5910.221280 | natural_scenes | 72.0 | 0.250211 | 4909 |
| 51357 | 9.0 | 5910.221280 | 5910.471491 | natural_scenes | 82.0 | 0.250211 | 4910 |
| 51358 | 9.0 | 5910.471491 | 5910.721702 | natural_scenes | 55.0 | 0.250211 | 4911 |
| 51359 | 9.0 | 5910.721702 | 5910.971898 | natural_scenes | 68.0 | 0.250197 | 4912 |
Receptive field mapping stimulus#
Because receptive field analysis is so central to interpreting results related to visual coding, every experiment in the Neuropixels Visual Coding dataset includes a standardized receptive field mapping stimulus. This stimulus is always shown at the beginning of the session, and uses the same parameters for every mouse.
We can look at the stimulus_presentations DataFrame in order to examine the
parameters of the receptive field mapping stimulus in more detail. The receptive
field mapping stimulus consists of drifting Gabor patches with a circular mask,
so we’re going to filter the DataFrame based on stimulus_name == 'gabors':
rf_stim_table = session.stimulus_presentations[session.stimulus_presentations.stimulus_name == 'gabors']
len(rf_stim_table)
3645
There are 3645 trials for the receptive field mapping stimulus. What combination of stimulus parameters is used across these trials? Let’s see which parameters actually vary for this stimulus:
keys = rf_stim_table.keys()
[key for key in keys if len(np.unique(rf_stim_table[key])) > 1]
['start_time',
'stop_time',
'x_position',
'orientation',
'y_position',
'duration',
'stimulus_condition_id']
We can ignore the parameters related to stimulus timing (start_time,
stop_time, and duration), as well as stimulus_condition_id, which is used
to find presentations with the same parameters. So we’re left with
orientation, x_position, and y_position.
print('Unique orientations : ' + str(list(np.sort(rf_stim_table.orientation.unique()))))
print('Unique x positions : ' + str(list(np.sort(rf_stim_table.x_position.unique()))))
print('Unique y positions : ' + str(list(np.sort(rf_stim_table.y_position.unique()))))
Unique orientations : [0.0, 45.0, 90.0]
Unique x positions : [-40.0, -30.0, -20.0, -10.0, 0.0, 10.0, 20.0, 30.0, 40.0]
Unique y positions : [-40.0, -30.0, -20.0, -10.0, 0.0, 10.0, 20.0, 30.0, 40.0]
We have 3 orientations and a 9 x 9 grid of spatial locations. Note that these locations are relative to the center of the screen, not the mouse’s center of gaze. How many repeats are there for each condition?
len(rf_stim_table) / (3 * 9 * 9)
15.0
This should match the number we get when dividing the length of the DataFrame by the total number of conditions:
len(rf_stim_table) / len(np.unique(rf_stim_table.stimulus_condition_id))
15.0
What about the drifting grating parameters that don’t vary, such as size (in degrees), spatial frequency (in cycles/degree), temporal frequency (in Hz), and contrast?
print('Spatial frequency: ' + str(rf_stim_table.spatial_frequency.unique()[0]))
print('Temporal frequency: ' + str(rf_stim_table.temporal_frequency.unique()[0]))
print('Size: ' + str(rf_stim_table['size'].unique()[0]))
print('Contrast: ' + str(rf_stim_table['contrast'].unique()[0]))
Spatial frequency: 0.08
Temporal frequency: 4.0
Size: [20.0, 20.0]
Contrast: 0.8
This stimulus is designed to drive neurons reliably across a wide variety of visual areas. Because of the large size (20 degree diameter), it lacks spatial precision. It also cannot be used to map on/off subfields on neurons. However, this is a reasonable compromise to allow us to map receptive fields with high reliability across all visual areas we’re recording from.
Now that we have a better understanding of the stimulus, let’s look at receptive fields for some neurons.
rf_stim_table.keys()
Index(['stimulus_block', 'start_time', 'stop_time', 'phase',
'spatial_frequency', 'x_position', 'temporal_frequency', 'color',
'stimulus_name', 'frame', 'contrast', 'orientation', 'size',
'y_position', 'duration', 'stimulus_condition_id'],
dtype='object')
Plotting receptive fields#
In order to visualize receptive fields, we’re going to use a function in the
ReceptiveFieldMapping class, one of the stimulus-specific analysis classes in
the AllenSDK. Let’s import it and create a rf_mapping object based on the
session we loaded earlier:
from allensdk.brain_observatory.ecephys.stimulus_analysis.receptive_field_mapping import ReceptiveFieldMapping
rf_mapping = ReceptiveFieldMapping(session)
The rf_mapping object contains a variety of methods related to receptive field
mapping. Its stim_table property holds the same DataFrame we created earlier.
rf_mapping.stim_table
| stimulus_block | start_time | stop_time | phase | spatial_frequency | x_position | temporal_frequency | stimulus_name | contrast | orientation | size | y_position | duration | stimulus_condition_id | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| stimulus_presentation_id | ||||||||||||||
| 1 | 0.0 | 84.804349 | 85.037870 | [3644.93333333, 3644.93333333] | 0.08 | -10.0 | 4.0 | gabors | 0.8 | 0.0 | [20.0, 20.0] | -40.0 | 0.233521 | 1 |
| 2 | 0.0 | 85.037870 | 85.288070 | [3644.93333333, 3644.93333333] | 0.08 | 30.0 | 4.0 | gabors | 0.8 | 0.0 | [20.0, 20.0] | 40.0 | 0.250201 | 2 |
| 3 | 0.0 | 85.288070 | 85.538271 | [3644.93333333, 3644.93333333] | 0.08 | 0.0 | 4.0 | gabors | 0.8 | 0.0 | [20.0, 20.0] | 0.0 | 0.250201 | 3 |
| 4 | 0.0 | 85.538271 | 85.788472 | [3644.93333333, 3644.93333333] | 0.08 | -20.0 | 4.0 | gabors | 0.8 | 45.0 | [20.0, 20.0] | 20.0 | 0.250201 | 4 |
| 5 | 0.0 | 85.788472 | 86.038686 | [3644.93333333, 3644.93333333] | 0.08 | -40.0 | 4.0 | gabors | 0.8 | 0.0 | [20.0, 20.0] | 40.0 | 0.250214 | 5 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 3641 | 0.0 | 995.598539 | 995.848745 | [3644.93333333, 3644.93333333] | 0.08 | 30.0 | 4.0 | gabors | 0.8 | 90.0 | [20.0, 20.0] | -10.0 | 0.250206 | 175 |
| 3642 | 0.0 | 995.848745 | 996.098950 | [3644.93333333, 3644.93333333] | 0.08 | 30.0 | 4.0 | gabors | 0.8 | 45.0 | [20.0, 20.0] | 10.0 | 0.250206 | 228 |
| 3643 | 0.0 | 996.098950 | 996.349156 | [3644.93333333, 3644.93333333] | 0.08 | 30.0 | 4.0 | gabors | 0.8 | 0.0 | [20.0, 20.0] | -20.0 | 0.250206 | 156 |
| 3644 | 0.0 | 996.349156 | 996.599362 | [3644.93333333, 3644.93333333] | 0.08 | 10.0 | 4.0 | gabors | 0.8 | 90.0 | [20.0, 20.0] | 20.0 | 0.250206 | 231 |
| 3645 | 0.0 | 996.599362 | 996.849568 | [3644.93333333, 3644.93333333] | 0.08 | -40.0 | 4.0 | gabors | 0.8 | 0.0 | [20.0, 20.0] | -30.0 | 0.250207 | 72 |
3645 rows × 14 columns
Before we calculate any receptive fields, let’s find some units in primary visual cortex (VISp) that are likely to show clear receptive fields:
v1_units = session.units[session.units.ecephys_structure_acronym == 'VISp']
Now, calculating the receptive field is as simple as calling
get_receptive_field() with a unit ID as the input argument.
RF = rf_mapping.get_receptive_field(v1_units.index.values[3])
This method creates a 2D histogram of spike counts at all 81 possible stimulus locations, and outputs it as a 9 x 9 matrix. It’s summing over all orientations, so each pixel contains the spike count across 45 trials.
To plot it, just display it as an image. The matrix is already in the correct orientation so that it matches the layout of the screen (e.g., the upper right pixel contains the spike count when the Gabor patch was in the upper right of the screen).
plt.figure(figsize=(5,5))
_ = plt.imshow(RF)
_ = plt.axis('off')

This particular unit has a receptive field that’s more or less in the center of the screen.
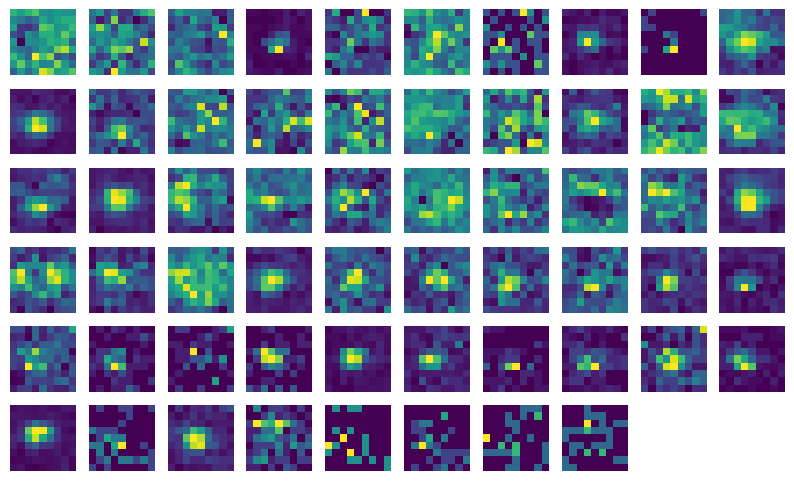
Let’s plot the receptive fields for all the units in V1:
def plot_rf(unit_id, index):
RF = rf_mapping.get_receptive_field(unit_id)
_ = plt.subplot(6,10,index+1)
_ = plt.imshow(RF)
_ = plt.axis('off')
_ = plt.figure(figsize=(10,6))
_ = [plot_rf(RF, index) for index, RF in enumerate(v1_units.index.values)]
Natural scenes stimulus#
Use the stimulus table for natural scenes to find all the times when a particular image is presented during the session, and add it to the plot of activity in V1. Pick the first image that was presented in this session.
stim_table_ns[stim_table_ns.frame==stim_table_ns.frame.iloc[0]].head()
| stimulus_block | start_time | stop_time | stimulus_name | frame | duration | stimulus_condition_id | |
|---|---|---|---|---|---|---|---|
| stimulus_presentation_id | |||||||
| 51355 | 9.0 | 5909.720859 | 5909.971070 | natural_scenes | 92.0 | 0.250211 | 4908 |
| 51494 | 9.0 | 5944.499911 | 5944.750122 | natural_scenes | 92.0 | 0.250211 | 4908 |
| 51637 | 9.0 | 5980.279805 | 5980.530018 | natural_scenes | 92.0 | 0.250213 | 4908 |
| 51686 | 9.0 | 5992.540056 | 5992.790262 | natural_scenes | 92.0 | 0.250206 | 4908 |
| 51735 | 9.0 | 6004.800292 | 6005.050501 | natural_scenes | 92.0 | 0.250209 | 4908 |
How many times was it presented?
len(stim_table_ns[stim_table_ns.frame==stim_table_ns.frame.iloc[0]])
50
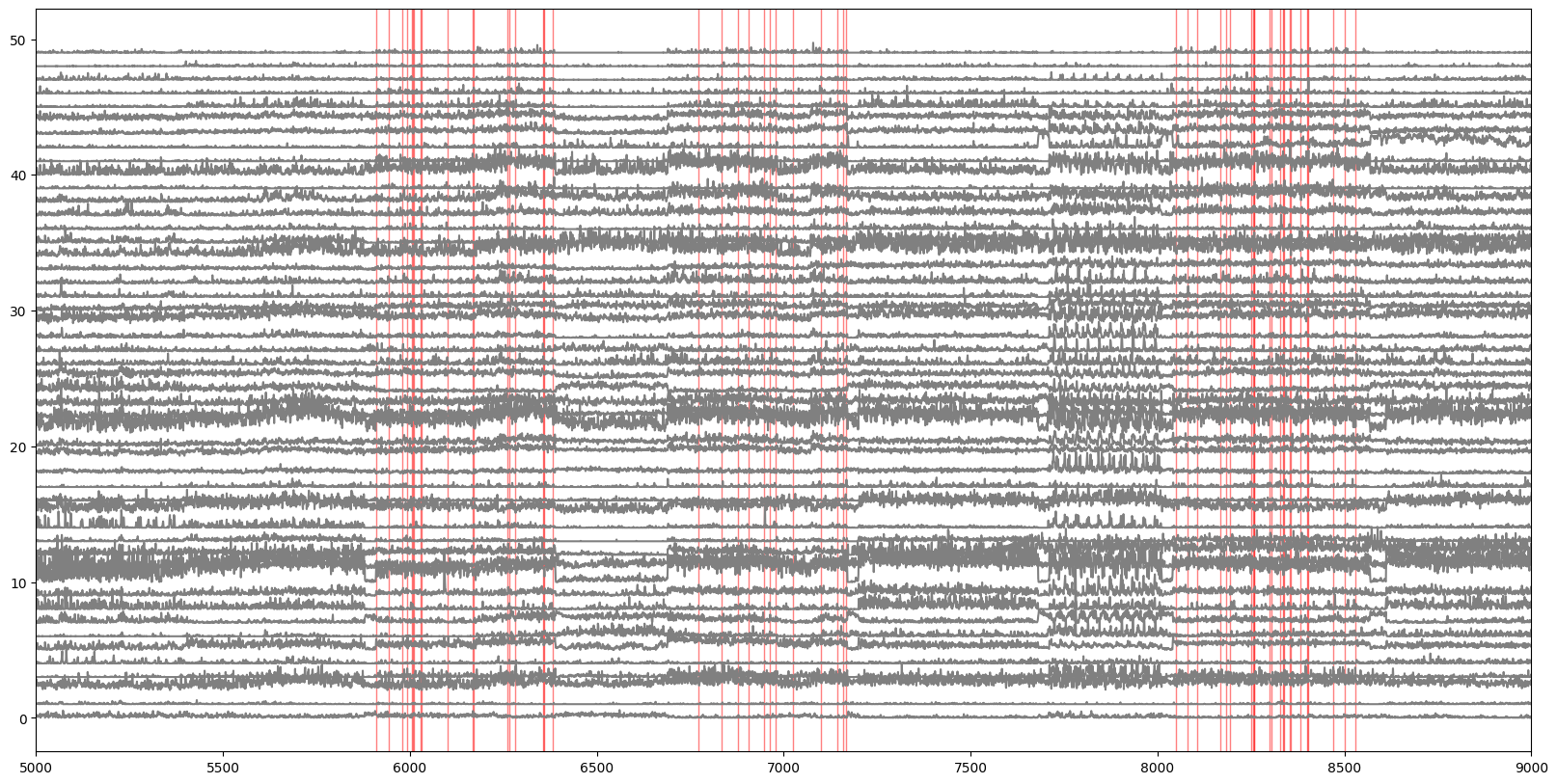
Mark the times when this particular scene was presented on our plot of the activity (without the epochs and running speed).
plt.figure(figsize=(20,10))
for i in range(numunits):
plt.plot(i+(v1_binned[i,:]/30.), color='gray')
stim_subset = stim_table_ns[stim_table_ns.frame==stim_table_ns.frame.iloc[0]]
for j in range(len(stim_subset)):
plt.axvspan(xmin=stim_subset.start_time.iloc[j], xmax=stim_subset.stop_time.iloc[j], color='r', alpha=0.5)
plt.xlim(5000,9000)
(5000.0, 9000.0)
Stimulus template#
What is this image? The stimulus template provides the images and movies that
were presented to the mouse. These are only provided for stimuli that are images
(natural scenes, natural movies) - parametric stimuli (eg. gratings) do not have
templates.
image_num = 96
image_template = cache.get_natural_scene_template(image_num)
plt.imshow(image_template, cmap='gray')
<matplotlib.image.AxesImage at 0x7f5846265420>

Example: Single trial raster plots for all units#
Now that we’ve seen the pieces of data, we can explore the neural activity in greater detail. Make a raster plot for a single presentation of the drifting grating stimulus at orientation = 45 degrees and temporal frequency = 2 Hz.
To start, make a function to make a raster plot of all the units in the experiment.
def plot_raster(spike_times, start, end):
num_units = len(spike_times)
ystep = 1 / num_units
ymin = 0
ymax = ystep
for unit_id, unit_spike_times in spike_times.items():
unit_spike_times = unit_spike_times[np.logical_and(unit_spike_times >= start, unit_spike_times < end)]
plt.vlines(unit_spike_times, ymin=ymin, ymax=ymax)
ymin += ystep
ymax += ystep
Find the first presentation of our chosen grating condition.
stim_table = session.get_stimulus_table(['drifting_gratings'])
subset = stim_table[(stim_table.orientation==45)&(stim_table.temporal_frequency==2)]
start = stim_table.start_time.iloc[0]
end = stim_table.stop_time.iloc[0]
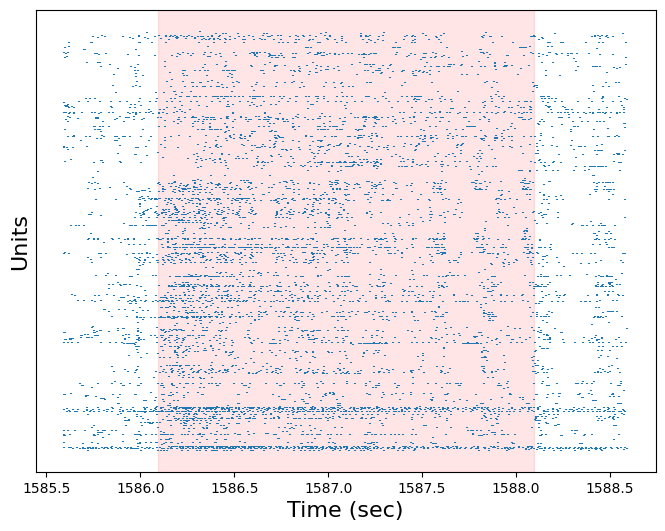
Use the plot_raster function to plot the response of all units to this trial. Pad the raster plot with half a second before and after the trial, and shade the trial red (with an alpha of 0.1)
plt.figure(figsize=(8,6))
plot_raster(session.spike_times, start-0.5, end+0.5)
plt.axvspan(start, end, color='red', alpha=0.1)
plt.xlabel('Time (sec)', fontsize=16)
plt.ylabel('Units', fontsize=16)
plt.tick_params(axis="y", labelleft=False, left=False)
plt.show()
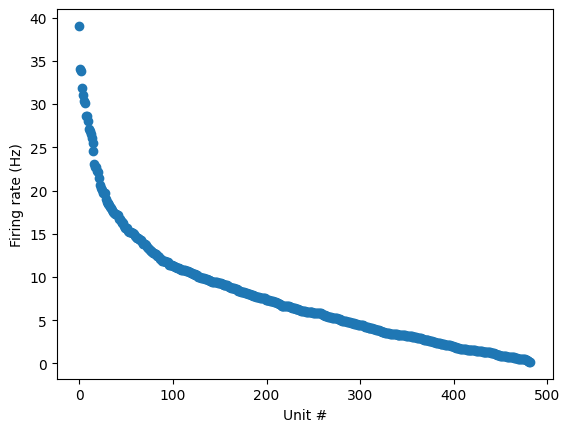
We can use the unit dataframe to arrange the neurons in the raster plot
according to their overall firing rate.
session.units.sort_values(by="firing_rate", ascending=False).head()
| waveform_PT_ratio | waveform_amplitude | amplitude_cutoff | cluster_id | cumulative_drift | d_prime | firing_rate | isi_violations | isolation_distance | L_ratio | ... | ecephys_structure_id | ecephys_structure_acronym | anterior_posterior_ccf_coordinate | dorsal_ventral_ccf_coordinate | left_right_ccf_coordinate | probe_description | location | probe_sampling_rate | probe_lfp_sampling_rate | probe_has_lfp_data | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| unit_id | |||||||||||||||||||||
| 951763835 | 0.475484 | 296.48580 | 0.000030 | 279 | 55.08 | 8.947122 | 39.043270 | 0.000051 | 170.093608 | 3.380263e-07 | ... | 394.0 | VISam | 7523 | 898 | 7531 | probeA | See electrode locations | 29999.970168 | 1249.998757 | True |
| 951769847 | 0.683558 | 187.32870 | 0.003021 | 2 | 124.35 | 5.695558 | 34.004900 | 0.011311 | 128.727591 | 3.679798e-04 | ... | 215.0 | APN | 7913 | 3209 | 7202 | probeB | See electrode locations | 29999.922149 | 1249.996756 | True |
| 951763130 | 0.609057 | 158.42424 | 0.055363 | 28 | 134.27 | 5.255101 | 33.830308 | 0.014039 | 136.299149 | 9.153142e-04 | ... | 1061.0 | PPT | 8205 | 2618 | 6750 | probeA | See electrode locations | 29999.970168 | 1249.998757 | True |
| 951763126 | 0.738584 | 260.37843 | 0.000051 | 26 | 121.95 | 6.741217 | 31.872133 | 0.002178 | 119.811105 | 2.618902e-04 | ... | 1061.0 | PPT | 8218 | 2646 | 6744 | probeA | See electrode locations | 29999.970168 | 1249.998757 | True |
| 951763434 | 0.593540 | 96.64278 | 0.000681 | 176 | 114.37 | 3.496612 | 31.058255 | 0.007283 | 124.356326 | 1.820049e-02 | ... | 382.0 | CA1 | 7719 | 1438 | 7110 | probeA | See electrode locations | 29999.970168 | 1249.998757 | True |
5 rows × 40 columns
plt.plot(session.units.sort_values(by="firing_rate", ascending=False).firing_rate.values, 'o')
plt.ylabel("Firing rate (Hz)")
plt.xlabel("Unit #")
Text(0.5, 0, 'Unit #')
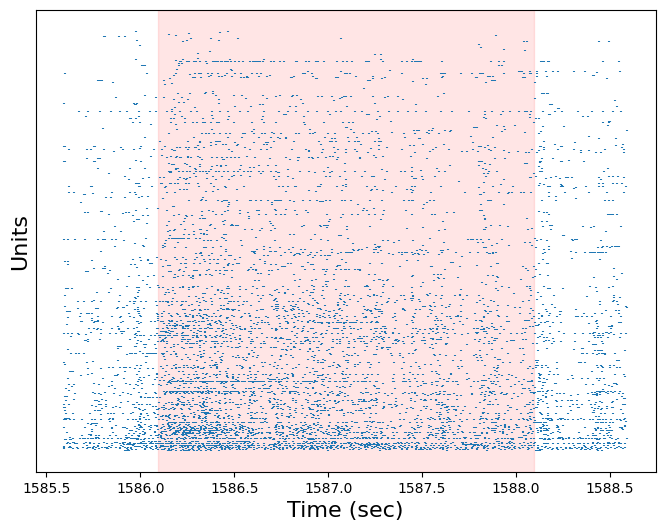
by_fr = session.units.sort_values(by="firing_rate", ascending=False)
spike_times_by_firing_rate = {
uid: session.spike_times[uid] for uid in by_fr.index.values
}
plt.figure(figsize=(8,6))
plot_raster(spike_times_by_firing_rate, start-0.5, end+0.5)
plt.axvspan(start, end, color='red', alpha=0.1)
plt.ylabel('Units', fontsize=16)
plt.xlabel('Time (sec)', fontsize=16)
plt.tick_params(axis="y", labelleft=False, left=False)
plt.show()
Stimulus responses#
A lot of the analysis of these data will requires comparing responses of neurons to different stimulus conditions and presentations. The SDK has functions to help access these, sorting the spike data into responses for each stimulus presentations and converting from spike times to binned spike counts. This spike histogram representation is more useful for many computations, since it can be treated as a timeseries and directly averaged across presentations.
The presentationwise_spike_counts provides the histograms for specified
stimulus presentation trials for specified units. The function requires
stimulus_presentation_ids for the stimulus in question, unit_ids for the
relevant units, and bin_edges to specify the time bins to count spikes in
(relative to stimulus onset).
The conditionwise_spike_statistics creates a summary of specified units
responses to specified stimulus conditions, including the mean spike count,
standard deviation, and standard error of the mean.
stim_table.head()
| stimulus_block | start_time | stop_time | phase | spatial_frequency | temporal_frequency | stimulus_name | contrast | orientation | size | duration | stimulus_condition_id | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| stimulus_presentation_id | ||||||||||||
| 3798 | 2.0 | 1586.091909 | 1588.093549 | [5308.98333333, 5308.98333333] | 0.04 | 4.0 | drifting_gratings | 0.8 | 270.0 | [250.0, 250.0] | 2.00164 | 246 |
| 3799 | 2.0 | 1589.094372 | 1591.096042 | [5308.98333333, 5308.98333333] | 0.04 | 4.0 | drifting_gratings | 0.8 | 135.0 | [250.0, 250.0] | 2.00167 | 247 |
| 3800 | 2.0 | 1592.096899 | 1594.098559 | [5308.98333333, 5308.98333333] | 0.04 | 8.0 | drifting_gratings | 0.8 | 180.0 | [250.0, 250.0] | 2.00166 | 248 |
| 3801 | 2.0 | 1595.099402 | 1597.101072 | [5308.98333333, 5308.98333333] | 0.04 | 4.0 | drifting_gratings | 0.8 | 270.0 | [250.0, 250.0] | 2.00167 | 246 |
| 3802 | 2.0 | 1598.101909 | 1600.103579 | [5308.98333333, 5308.98333333] | 0.04 | 1.0 | drifting_gratings | 0.8 | 180.0 | [250.0, 250.0] | 2.00167 | 249 |
# specify the time bins in seconds, relative to stimulus onset
time_step = 1/100.
duration = stim_table.duration.iloc[0]
time_domain = np.arange(0, duration+time_step, time_step)
print(time_domain.shape)
(202,)
stim_ids = stim_table[(stim_table.orientation==90)&(stim_table.temporal_frequency==1)].index
print(stim_ids.shape)
(15,)
histograms = session.presentationwise_spike_counts(bin_edges=time_domain,
stimulus_presentation_ids=stim_ids,
unit_ids=v1_units.index)
What type of object is this? What is its shape?
type(histograms)
xarray.core.dataarray.DataArray
histograms.shape
(15, 201, 58)
Xarray#
This has returned a new (to this notebook) data structure, the
xarray.DataArray. You can think of this as similar to a 3+D
pandas.DataFrame, or as a numpy.ndarray with labeled axes and indices. See
the xarray documentation for
more information. In the mean time, the salient features are:
Dimensions : Each axis on each data variable is associated with a named dimension. This lets us see unambiguously what the axes of our array mean.
Coordinates : Arrays of labels for each sample on each dimension.
xarray is nice because it forces code to be explicit about dimensions and coordinates, improving readability and avoiding bugs. However, you can always convert to numpy or pandas data structures as follows:
to pandas:
histograms.to_dataframe()produces a multiindexed dataframeto numpy:
histograms.valuesgives you access to the underlying numpy array
Example: Plot the unit’s response
Plot the response of the first unit to all 15 trials.
for i in range(15):
plt.plot(histograms.time_relative_to_stimulus_onset, i+histograms[i,:,0])
plt.xlabel("Time (s)", fontsize=16)
plt.ylabel("Trials", fontsize=16)
Text(0, 0.5, 'Trials')
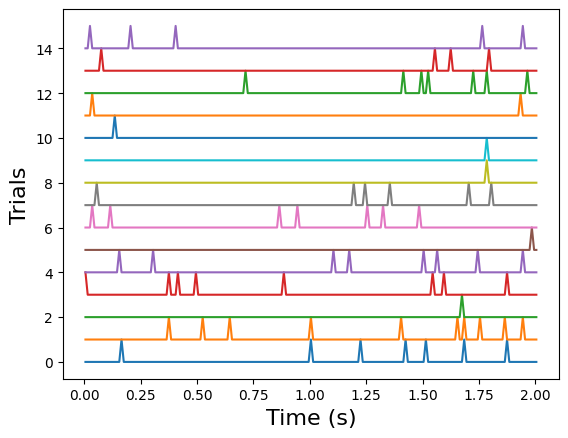
Example: Compute the average response over trials for all units
Plot a heatmap of mean response for all units in V1.
mean_histograms = histograms.mean(dim="stimulus_presentation_id")
mean_histograms.coords
Coordinates:
* time_relative_to_stimulus_onset (time_relative_to_stimulus_onset) float64 ...
* unit_id (unit_id) int64 951762582 ... 951762972
import xarray.plot as xrplot
xrplot.imshow(darray=mean_histograms, x="time_relative_to_stimulus_onset",
y="unit_id")
<matplotlib.image.AxesImage at 0x7f584afab400>
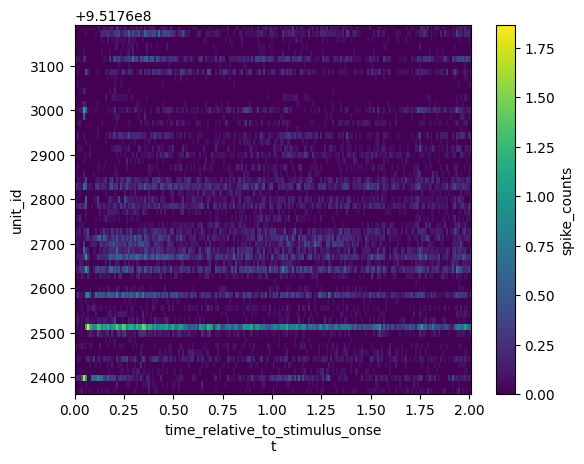
Example: Conditionwise analysis
In order to compute a tuning curve that summarizes the responses of a unit to
each stimulus condition of a stimulus, use the conditionwise_spike_statistics
to summarize the activity of specific units to the different stimulus
conditions.
stim_ids = stim_table.index.values
dg_stats = session.conditionwise_spike_statistics(stimulus_presentation_ids=stim_ids, unit_ids=v1_units.index)
What type of object is this? What is its shape?
type(dg_stats)
pandas.core.frame.DataFrame
dg_stats.shape
(2378, 5)
What are its columns?
dg_stats.columns
Index(['spike_count', 'stimulus_presentation_count', 'spike_mean', 'spike_std',
'spike_sem'],
dtype='object')
Can you explain the first dimension?
dg_stats.head()
| spike_count | stimulus_presentation_count | spike_mean | spike_std | spike_sem | ||
|---|---|---|---|---|---|---|
| unit_id | stimulus_condition_id | |||||
| 951762582 | 246 | 87 | 15 | 5.800000 | 3.967727 | 1.024463 |
| 951762586 | 246 | 311 | 15 | 20.733333 | 7.601378 | 1.962667 |
| 951762598 | 246 | 65 | 15 | 4.333333 | 5.984106 | 1.545090 |
| 951762602 | 246 | 5 | 15 | 0.333333 | 0.617213 | 0.159364 |
| 951762624 | 246 | 331 | 15 | 22.066667 | 9.129753 | 2.357292 |
Example: Merge the conditionwise statistics with stimulus information
In order to link the stimulus responses with the stimulus conditions, merge the
spike_statistics output with the stimulus table using pd.merge().
dg_stats_stim = pd.merge(
dg_stats.reset_index().set_index(['stimulus_condition_id']),
session.stimulus_conditions,
on=['stimulus_condition_id']
).reset_index().set_index(['unit_id', 'stimulus_condition_id'])
This dataframe currently has a multi-index, meaning that each row is indexed by the pair of unit_id and stimulus_condition_id, rather than a single identifier. There are several ways to use this index:
specify the pair of identifiers as a tuple:
dg_stats_stim.loc[(unit_id, stim_id)]specifying the axis makes it easier to get all rows for one unit:
dg_stats_stim.loc(axis=0)[unit_id, :]or you can use
dg_stats_stim.reset_index()to move the index to regular columns
dg_stats_stim.head()
| spike_count | stimulus_presentation_count | spike_mean | spike_std | spike_sem | phase | spatial_frequency | x_position | temporal_frequency | mask | color | stimulus_name | units | opacity | frame | contrast | orientation | size | y_position | color_triplet | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| unit_id | stimulus_condition_id | ||||||||||||||||||||
| 951762582 | 246 | 87 | 15 | 5.800000 | 3.967727 | 1.024463 | [5308.98333333, 5308.98333333] | 0.04 | null | 4.0 | None | null | drifting_gratings | deg | True | null | 0.8 | 270.0 | [250.0, 250.0] | null | [1.0, 1.0, 1.0] |
| 951762586 | 246 | 311 | 15 | 20.733333 | 7.601378 | 1.962667 | [5308.98333333, 5308.98333333] | 0.04 | null | 4.0 | None | null | drifting_gratings | deg | True | null | 0.8 | 270.0 | [250.0, 250.0] | null | [1.0, 1.0, 1.0] |
| 951762598 | 246 | 65 | 15 | 4.333333 | 5.984106 | 1.545090 | [5308.98333333, 5308.98333333] | 0.04 | null | 4.0 | None | null | drifting_gratings | deg | True | null | 0.8 | 270.0 | [250.0, 250.0] | null | [1.0, 1.0, 1.0] |
| 951762602 | 246 | 5 | 15 | 0.333333 | 0.617213 | 0.159364 | [5308.98333333, 5308.98333333] | 0.04 | null | 4.0 | None | null | drifting_gratings | deg | True | null | 0.8 | 270.0 | [250.0, 250.0] | null | [1.0, 1.0, 1.0] |
| 951762624 | 246 | 331 | 15 | 22.066667 | 9.129753 | 2.357292 | [5308.98333333, 5308.98333333] | 0.04 | null | 4.0 | None | null | drifting_gratings | deg | True | null | 0.8 | 270.0 | [250.0, 250.0] | null | [1.0, 1.0, 1.0] |
Tuning curve#
Let’s plot a 2D tuning curve for the first unit, comparing responses across temporal frequency and orientation.
unit_id = v1_units.index[1]
stim_ids = stim_table.index.values
session.get_stimulus_parameter_values(stimulus_presentation_ids=stim_ids, drop_nulls=True)
{'phase': array(['[5308.98333333, 5308.98333333]'], dtype=object),
'spatial_frequency': array(['0.04'], dtype=object),
'temporal_frequency': array([4.0, 8.0, 1.0, 2.0, 15.0], dtype=object),
'contrast': array([0.8], dtype=object),
'orientation': array([270.0, 135.0, 180.0, 0.0, 90.0, 225.0, 45.0, 315.0], dtype=object),
'size': array(['[250.0, 250.0]'], dtype=object)}
orivals = session.get_stimulus_parameter_values(stimulus_presentation_ids=stim_ids, drop_nulls=True)['orientation']
tfvals = session.get_stimulus_parameter_values(stimulus_presentation_ids=stim_ids, drop_nulls=True)['temporal_frequency']
response_mean = np.empty((len(orivals), len(tfvals)))
response_sem = np.empty((len(orivals), len(tfvals)))
for i,ori in enumerate(orivals):
for j,tf in enumerate(tfvals):
stim_id = stim_table[(stim_table.orientation==ori)&(stim_table.temporal_frequency==tf)].stimulus_condition_id.iloc[0]
response_mean[i,j] = dg_stats_stim.loc[(unit_id, stim_id)].spike_mean
response_sem[i,j] = dg_stats_stim.loc[(unit_id, stim_id)].spike_sem
plt.imshow(response_mean)
plt.xlabel("Temporal frequency (Hz)")
plt.ylabel("Direction (deg)")
plt.xticks(range(5), tfvals)
plt.yticks(range(8), orivals)
plt.show()
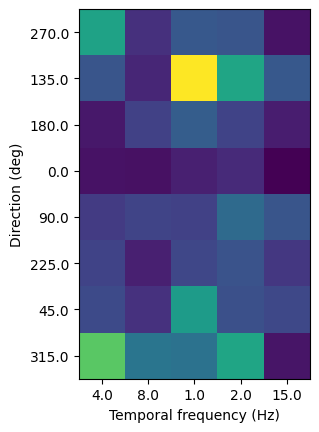
Precomputed metrics#
This section is not yet complete, but you can use the precomputed metrics provided by the AllenSDK as is described in Precomputed stimulus metrics.
